Yagi with 5 mm element diameter
This 10 element design, BSZ10.NEC is now in use as the vertical part of the SM5FRH cross yagi system. The vertical elements sit in front of the stacking harness so the vertical antenna uses only slightly more than half the boom length of the horizontal array. The difference in gain between the horisontal and vertical array is only about 1dB because of the high degree of optimisation for this antenna.
The behaviour of the original NEC2 for the 10 element design is displayed in the figures below, you may also look at the numerical data
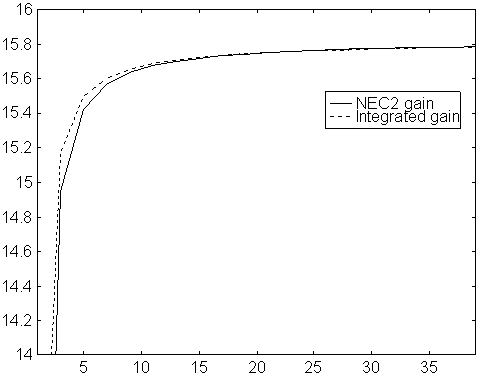
Fig 1. Gain vs number of segments per element.
Original NEC2 for a 10 element yagi with 5mm elements
on 144MHz.
The gain is calculated in two ways.
The solid line is gain as obtained directly from NEC2,
calculated from the absolute value of the far
field in the forward direction.
The dotted line is the gain as calculated from the
far field in the forward direction divided by the
average far field.
The dotted line includes ohmic losses.
.
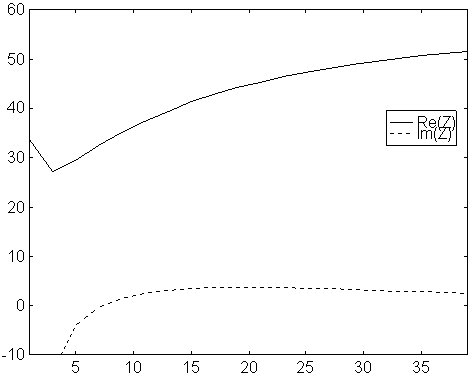
Fig 2. Feed point impedance vs number of segments per element.
Original NEC2 for a 10 element yagi with 5mm elements
on 144MHz. Solid line is real part and dotted
line is imaginary part.
Note that this design with 5mm elements is much better modelled by NEC2 than the less critical design with 9mm elements. NEC2 is for thin wires!!
The behaviour of the modified NEC2 for the 10 element design is displayed in the figures below, you may also look at the numerical data
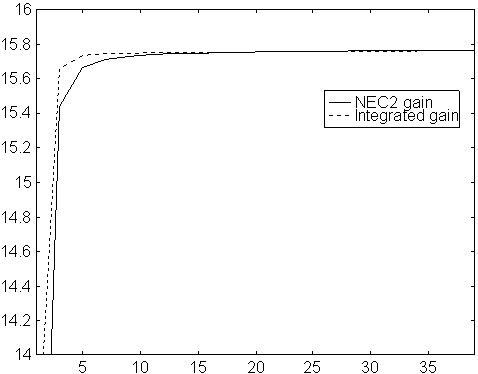
Fig 3. Gain vs number of segments per element.
Modified NEC2 for a 10 element yagi with 5mm elements
on 144MHz.
The gain is calculated in two ways.
The solid line is gain as obtained directly from NEC2,
calculated from the absolute value of the far
field in the forward direction.
The dotted line is the gain as calculated from the
far field in the forward direction divided by the
average far field.
The dotted line includes ohmic losses.
.
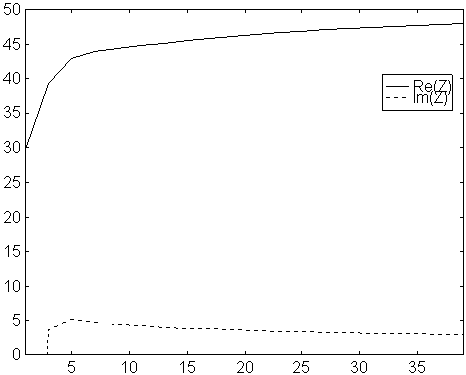
Fig 4. Feed point impedance vs number of segments per element.
Modified NEC2 for a 10 element yagi with 5mm elements
on 144MHz. Solid line is real part and dotted
line is imaginary part.
The modified version of NEC2 is an improvement over the original program also for this 10 element yagi with 5 mm elements. The difference is small, but making a pre optimisation with only 3 segments per element may save time, and will be much better in the modified version.
Single Dipole
As a further illustration, look at these calculations of a single dipole, for which the length is selected to give a purely resistive feed impedance when calculated using 15 segments in original NEC2.
Impedances
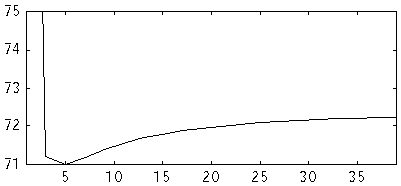
Fig 5. NEC2 Re Z (ohm) versus number of segments at 144 MHz
for a dipole. D=10 mm. L=973.514
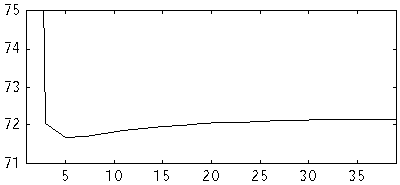
Fig 6. Modified NEC Re Z (ohm) versus number of segments at 144 MHz
for a dipole. D=10 mm. L=973.514
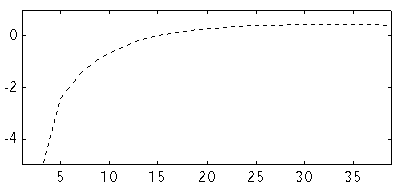
Fig 7. NEC2 Im Z (ohm) versus number of segments at 144 MHz for a dipole. D=10 mm. L=973.514
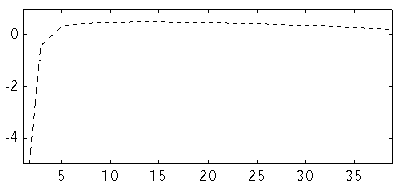
Fig 8. Modified NEC Im Z (ohm) versus number
of segments at 144 MHz
for a dipole. D=10 mm. L=973.514
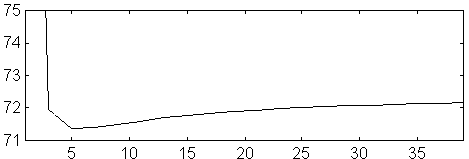
Fig 9. NEC2 Re Z (ohm) versus number of segments at 144 MHz for a dipole. D=5 mm. L=985.127
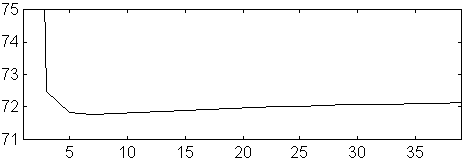
Fig 10. Modified NEC Re Z (ohm) versus number of segments at 144 MHz for a dipole. D=5 mm. L=985.127
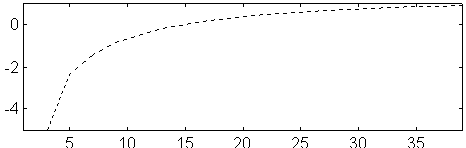
Fig 11. NEC2 Im Z (ohm) versus number of segments at 144 MHz for a dipole. D=5 mm. L=985.127
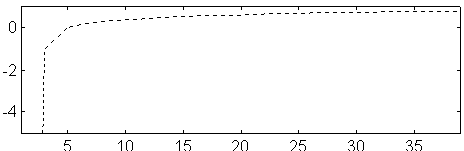
Fig 12. Modified NEC Im Z (ohm) versus number of segments at 144 MHz
for a dipole. D=5 mm. L=985.127
The imaginary part of the impedance is a measure of the electrical length of the dipole. When we use a computer model to find the optimum antenna for certain criteria it is important to use a model for which it is possible to evaluate the systematic errors when the model antenna is to be realised in the physical world.
If the model produces an electrical length that is independent of the number of segments for each element, we can expect the systematic errors to be only a constant, maybe 3 mm, to remove from all elements, provided they have the same diameter. Otherwise we would expect a second correction, that would depend on the segment or the element length.
In NEC2 the gain is calculated from the absolute value of the far field. The formula used is a simplified one. It just uses a current element at the center of each segment instead of the cosine current distribution that is used for short range field computations. This leads to a systematic error in all NEC2 gain calculations when few segments are used.
The systematic error is in the level of the far field, but the lobe pattern is nearly correct - a current element is a dipole radiator - therefore, the gain figure calculated from the radiation pattern is nearly correct even with only 1 segment on each element.
The gain as calculated from the radiation pattern is the number maximised by OMNEC. The behaviour of the gain of a dipole for different numbers of segments supports the use of very few segments when optimising large structures.
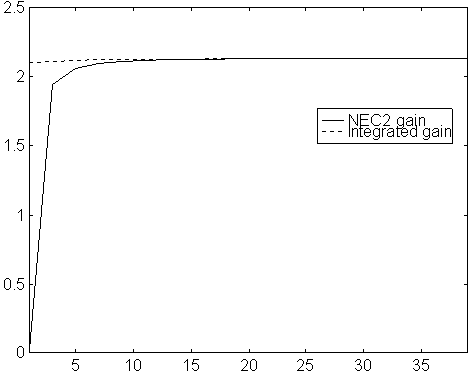
Fig 13. Gain versus number of segments for a half wave
dipole.
The gain versus number of segments looks very similar
for NEC2 and modified NEC, regardless of element diameter.
If you are interested in details, look at these tables
of gain and impedances for dipoles at 144MHz
for different numbers of segments:
NEC2, diam 5 mm, length 985.127 mm
Modifed NEC, diam 5 mm, length 985.127 mm
NEC2, diam 10 mm, length 973.514 mm
Modifed NEC, diam 10 mm, length 985.127 mm